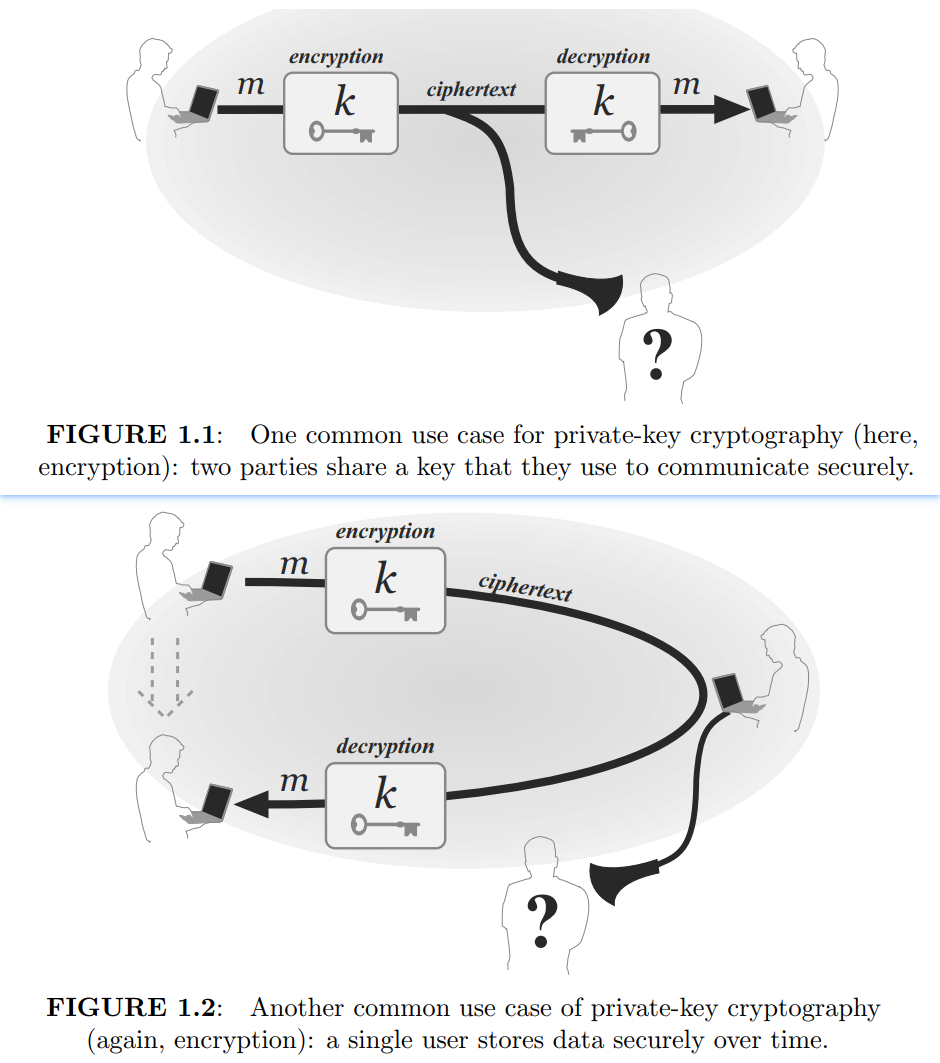
Reading Notes // IMC 1.3

Caesar’s cipher

Julius Caesar encrypted by shifting the letters of the alphabet 3 places forward
- begin the attack now → EHJLQWKHDWWDFNQRZ

The shift cipher and the sufficient key-space principle

The shift cipher

Definition
- Specifically, in the shift cipher the key k is a number between 0 and 25. To encrypt, letters are shifted as in Caesar’s cipher, but now by k places.
Algorithms
- Algorithm Gen outputs a uniform key $k \in {0, …, 25}$;
- algorithm Enc takes a key k and a plaintext and shifts each letter of the plaintext forward k positions (wrapping around at the end of the alphabet);
- algorithm Dec takes a key k and a ciphertext and shifts every letter of the ciphertext backward k positions
A more mathematical description

sufficient key-space principle

An attack that involves trying every possible key is called a brute-force or exhaustive-search attack.
sufficient key-space principle：
- Any secure encryption scheme must have a key space that is sufficiently large to make an exhaustive-search attack infeasible.

The mono-alphabetic substitution cipher

Definition
- In the mono-alphabetic substitution cipher the key also defines a map on the alphabet, but the map is now allowed to be arbitrary subject only to the constraint that it be one-to-one (so that decryption is possible).
Example
- tellhimaboutme → GDOOKVCXEFLGCD
Key space
- Assuming the English alphabet is being used, the key space is of size 26! =26·25·24 · ·· 2·1, or approximately $2^{88}$, and a brute-force attack is infeasible.
- This, however, does not mean the cipher is secure!
attack
- The mono-alphabetic substitution cipher can then be attacked by utilizing statistical properties of the English language.
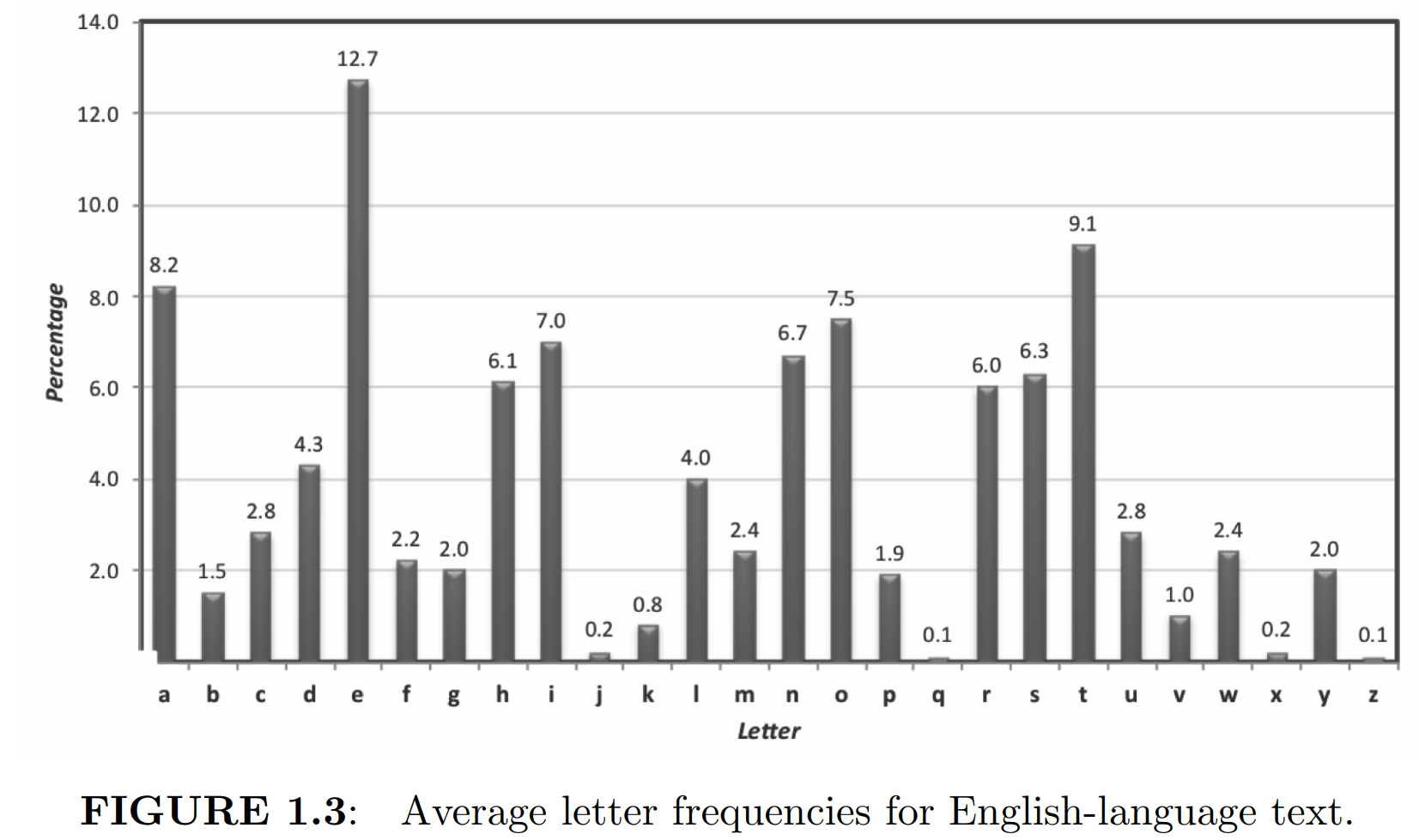
- P.S. utilizing other knowledge of English, such as the fact that q is generally followed by u, and that h is likely to appear between t and e
exercise
- JGRMQOYGHMVBJWRWQFPWHGFFDQGFPFZRKBEEBJIZQQOCIBZKLFAFGQVFZFWWE OGWOPFGFHWOLPHLRLOLFDMFGQWBLWBWQOLKFWBYLBLYLFSFLJGRMQBOLWJVFP FWQVHQWFFPQOQVFPQOCFPOGFWFJIGFQVHLHLROQVFGWJVFPFOLFHGQVQVFILE OGQILHQFQGIQVVOSFAFGBWQVHQWIJVWJVFPFWHGFIWIHZZRQGBABHZQOCGFHX

An improved attack on the shift cipher.

Previous attack on the shift cipher
- required decrypting the ciphertext using each possible key, and then checking which key results in a plaintext that “makes sense”
- drawback: difficult for a computer to check whether a given plaintext “makes sense”
- a special case that will make our previous attack useless: the plaintext characters follow the same distribution as English-language text even though the plaintext itself is not valid English
An improved attack
- First, associate the letters of the English alphabet with 0, …, 25.
- $p_i$: the frequency of the i-th letter in normal English text
  
  $\sum_{i=0}^{25}p_{i}^{2}\approx0.065.$
- $q_i$: the frequency of the ith letter of the alphabet in this ciphertext
- If the key is $k$, then $p_i$ should be roughly equal to $q_{i+k}$ for all $i$ because the $i$-th letter is mapped to the $(i + k)$-th letter.
- if we compute for each value of $j \in {0, …, 25}$:
  
  $I_{j}\ {\stackrel{\mathrm{def}}{=}}\ \sum_{i=0}^{25}p_{i}\cdot q_{i+j}$
  
  then we expect to find that $I_k \approx 0.065$, that $k$ is $j$

The Vigenere (poly-alphabetic shift) cipher

poly-alphabetic shift cipher

a key might map the 2-character block ab to DZ while mapping ac to TY
the plaintext character a does not get mapped to a fixed ciphertext character
Poly-alphabetic substitution ciphers make it harder to perform statistical analysis

key

The key is now viewed as a string of letters; encryption is done by shifting each plaintext character by the amount indicated by the next character of the key

Attacking the Vigenere cipher

if the length of the key is known then attacking the cipher is relatively easy
- Assume the key $k$ is $k=k_1\cdots k_t$
- Divide ciphertext into $t$ parts, for all $j \in {1, \cdots, t}$, the ciphertext characters $c_j, c_{j+t}, c_{j+2t}, …$ all resulted by shifting the corresponding plaintext by $k_t$ positions. This is called $j$-th stream. We have $t$ streams in total.
- Determine which of the 26 possible shifts was used for these $t$ streams respectively.
  - Attack 1:
    - tabulate the frequency of each ciphertext character and then check which of the 26 possible shifts yields the \right” probability distribution for that stream.
    - time: 26 · t
  - Attack 2:
    - apply the improved attack on the shift cipher (discussed earlier) to each stream
What if the key length is unknown
- as long as the maximum length T of the key is not too large, we can simply repeat the above attack T times (once for each possible value $t \in {1, \cdots, t}$)
- Kasiski’s method
- identify repeated patterns of length 2 or 3 in the ciphertext. These are likely the result of certain bigrams or trigrams that appear frequently in the plaintext.
- For example, consider the common word “the.” This word will be mapped to different ciphertext characters, depending on its position in the plaintext. However, if it appears twice in the same relative position, then it will be mapped to the same ciphertext characters. For a sufficiently long plaintext, there is thus a good chance that “the” will be mapped repeatedly to the same ciphertext characters.
- Therefore, the greatest common divisor of the distances between repeated sequences (assuming they are not coincidental) will yield the key length $t$ or a multiple thereof.
  
  In the above example, the period is 5 and the distance between the two appearances of LII is 30, which is 6 times the period.
- index of coincidence method
  - Recall that if the key length is t, the first stream: $c_{1},,c_{1+t},,c_{1+2t},,\cdot,\cdot,\cdot$
    
    these characters use the same shift
  - $q_i$: the observed frequency of the $i$-th alphabet letter in the first stream
  - If the shift for the first stream is $j$, then we expect $q_{i+j},\approx,p_{i}$
  - As a consequence: $\sum_{i=0}^{25}q_{i}^{2}\approx\sum_{i=0}^{25}p_{i}^{2}\approx0.065$
  - So a nice way to determine the key length is we try every possible value in the range, and find when this sum $S_{\tau}\ {\stackrel{\mathrm{def}}{=}}\ \sum_{i=0}^{25}q_{i}^{2}$ is approximately 0.065.
  - After we find a possible key length using the first stream, we can validate it using the second stream
- Ciphertext length and cryptanalytic attacks
  - The above attacks on the Vigenere cipher require a longer ciphertext than the attacks on previous schemes.
    - the index of coincidence method requires the stream to be sufficiently long in order to ensure that the observed frequencies are close to what is expected
  - This illustrates that a longer key can, in general, require the cryptanalyst to obtain more ciphertext in order to carry out an attack.
  - P.S. the Vigenere cipher can be shown to be secure if the key is as long as what is being encrypted